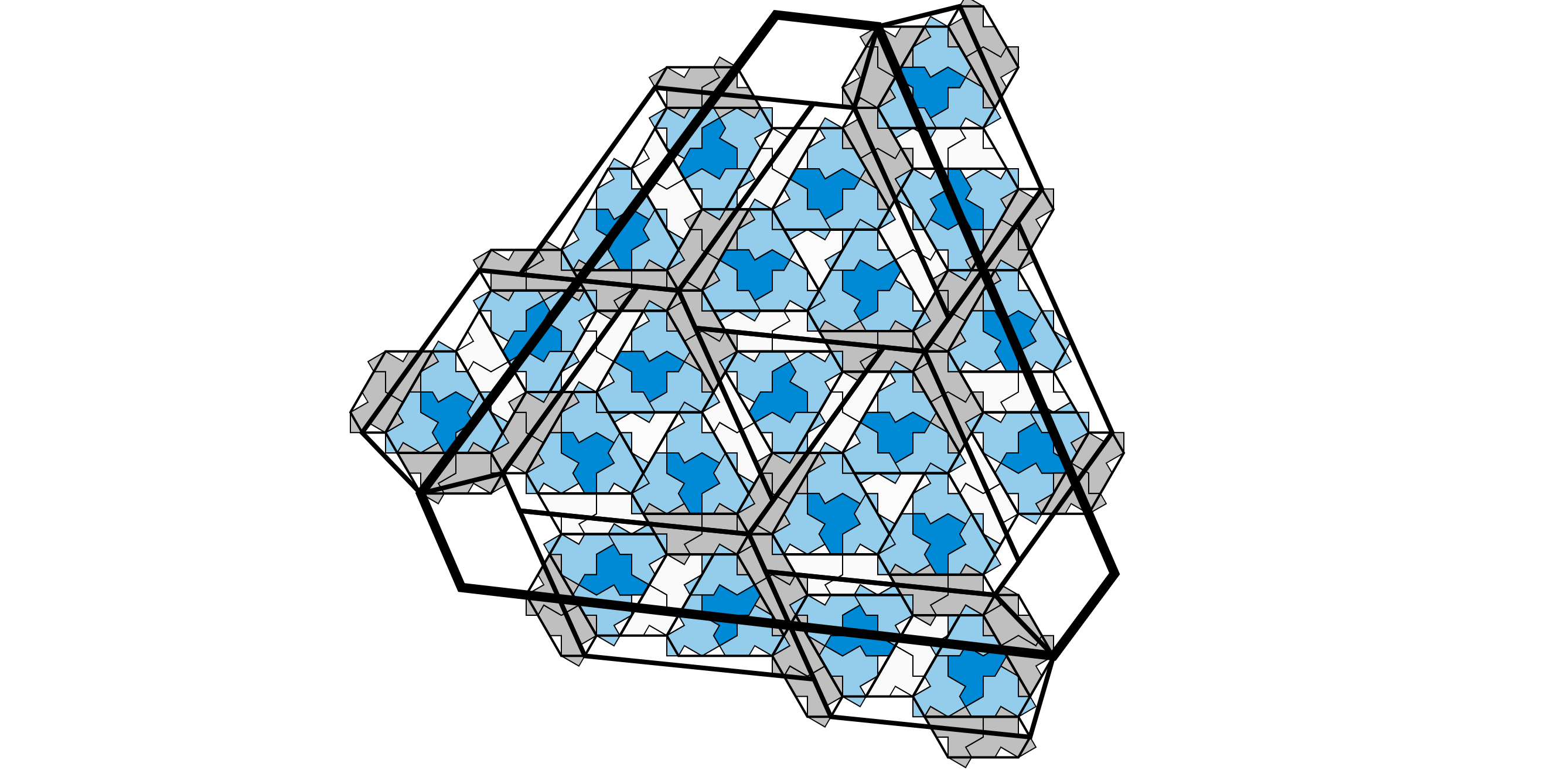
Computer scientists found the holy grail of tiles. They call it the “einstein,” one shape that alone can cover a plane without ever repeating a pattern.
And all it takes for this special shape is 13 sides.
In the world of mathematics, an “aperiodic monotile”—also known as an einstein based off a German phrase for one stone—is a shape that can tile a plane, but never repeat.
“In this paper we present the first true aperiodic monotile, a shape that forces aperiodicity through geometry alone, with no additional constrains applied via matching conditions,” writes Craig Kaplan, a computer science professor from the University of Waterloo and one of the four authors of the paper. “We prove that this shape, a polykite that we call ‘the hat,’ must assemble into tilings based on a substitution system.”
[…]
The history of the aperiodic tile has never had a breakthrough like this one. The first aperiodic sets had over 20,000 tiles, Kaplan tweets. “Subsequent research lowered that number, to sets of size 92, then six, and then two in the form of the famous Penrose tiles.” But those Penrose tiles were from 1974.
[…]
The team proved the nature of the shape through computer coding, and in a fascinating aside, the shape doesn’t lose its aperiodic nature even when the length of sides changes.
“We finally,” Kaplan says, “got down to one!”
It’s time for that bathroom remodel.
Source: Researchers Discovered a New 13-Sided Shape

Robin Edgar
Organisational Structures | Technology and Science | Military, IT and Lifestyle consultancy | Social, Broadcast & Cross Media | Flying aircraft